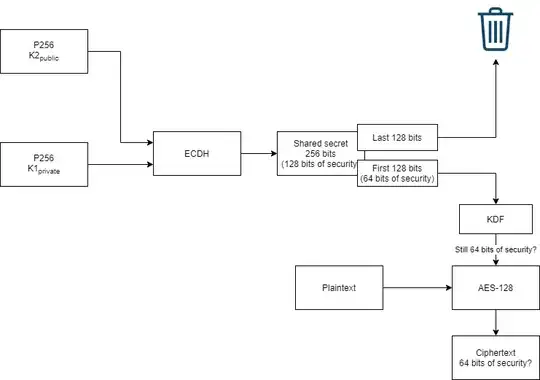
First of all, generally, the shared secret is split in half because it consists of an X and Y coordinate. It is after all the point resulting in multiplying a public key point with a private key / vector, resulting in another point on the curve. Now the X and Y coordinate are related, so generally, only the X coordinate is used as a shared secret.
Currently, you are assuming that the total result is 256 bits. However, for Elliptic Curves, each coordinate of the curve is 256 bits, making a total of 512 bits. So generally you would be left with 256 bits - not 128 bits - once you split the full outcome of the ECDH key agreement. I'd make sure if that's not what is meant because it would make a whole lot more sense. Please make sure that the result is precisely 64 bytes in that case (if it is more then the header should be removed in such a way that a 64-byte X-coordinate is left - how depends on the format of the point that is generated).
Furthermore, the (classic) security of ECDH with a key size of 256 bits is 128 bits because that's what level of security finite field will produce. It is an indication of the security in bits (compared to e.g. AES) that ECDH produces. However, that doesn't mean that the X-coordinate is not well distributed; to my knowledge it is. So even if you would split the X-coordinate in half you'd still be left with 128 bits of security. Finally, even if there would be an algorithmic weakness then the one-way property of the KDF would, with a very high degree of certainty, remove such weaknesses.
All that said: if indeed 128 bits are used instead of 256 then the protocol doesn't make all that much sense. Using the full 256 bits of a (constant sized) X-coordinate should be preferred.
Notes:
- I'd use AES-256 instead of AES-128 and also generate a random IV where required;
- 256-bit curves only provide 128-bit security against classical crypto-analysis, full-fledged quantum computers would certainly reduce that by a significant amount, rendering the algorithm insecure.