When it comes to asymmetric cryptosystems like RSA and ECC, security in bits is not the figure quoted in bits for key size (which itself has no universal relationship with the number of bits in the actual form taken by either the public or private key, which I won't further discuss in this answer).
Oversimplifying, and sticking to attacks using classical computers (because quantum computers usable for cryptanalysis are only an uncertain possibility for a remote future)
- $n$-bit security means that $2^n$ operations of some kind are believed needed on a classical computer to attack the system from ciphertext or other intercepted data. 96-bit security seems practically secure today (even 80-bit was never broken in a public attack), and each additional bit doubles the difficulty, making 128-bit safe for perhaps one or more decades, depending on one's wilderness of imagination. Anything above is for long-term security, or as a margin for attacks not envisioned in evaluation of the security level.
- With ECC, $n$-bit security requires a curve on a finite field which elements need at least about $2n$ bits for their representation, and that $2n$-bit field size is usually what's quoted as size or key size. Thus 256-bit ECC gives at most about 128-bit security, 521-bit ECC gives at most about 260-bit security, rounded to 256-bit because that's a common symmetric key size.
- With RSA, the public modulus size as found in (or derivable from) the public key is what's quoted as size, or key size (like, 2048-bit or 15360-bit). Its relationship to security level is more complex than in ECC. NIST SP 800-57 Pt 1 gives these very rough figures, which indeed tell (bottom line, leftmost and two rightmost columns) that 256-bit security is roughly obtained for 15360-bit RSA or 521-bit ECC.
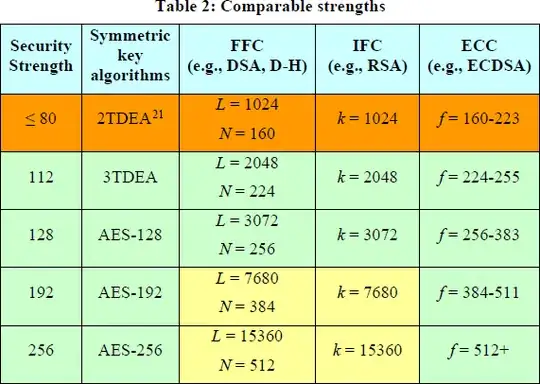
Is there a really much difference between 128bits 256bit and 512bits as it comes to security implemented in messaging apps or is t more important the way it has been implemented?
For data becoming of no value after less than a decade, there is not really much difference between 128-bit security and higher grades (but in the unlikely case that in the above "128bit" was an ECC field size, or if any of "128bits 256bit and 512bits" was an RSA modulus size, these numbers would be too low for decent security).
For key sizes giving decent security level (with the limit perhaps somewhere between 72 to 112-bit security these days depending on a variety of factors), what matters most to security of a messaging apps is who can get at the keys and ancillary data (like, most importantly, who communicates with who), what's done with the crypto, and the quality of the implementation.
