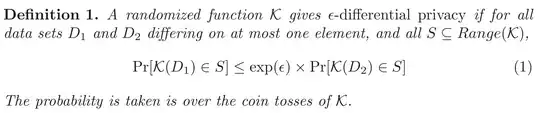I don't understand what does it mean by "The probability is taken is over the coin tosses of K."
Does it mean, the probability distribution is generated based on exactly same data but only the function is selected randomly?
So it's the data that ensures the differential privacy instead of the function, right?
No, it means that the functions are chosen from some domain with some probability distribution. This is standard for randomized algorithms.
For simplicity, assume there are $N$ randomized functions $\mathcal{K}$ possible, and one choose one uniformly with probability $1/N.$
For example, if we restricted ourselves to polynomials of degree $\leq k$ over $GF(q),$ there would be $N=q^{k+1}$ such possible functions and we choose a function by uniformly choosing each of its $k+1$ coordinates from $GF(q)$, thus with probability $q^{-(k+1)}.$
In this case the probability expression just means that $$ \frac{\#\{\mathcal{K}: \mathcal{K}(D_1) \in S\}}{N}\leq \exp(\epsilon)\frac{\#\{\mathcal{K}: \mathcal{K}(D_2) \in S\}}{N}, $$ and of course $N$ can be cancelled in the two sides of this equation. In general, the distribution may of course not be exactly uniform.
Differential privacy is a property of an algorithm (or if you like, a probability distribution over functions), not a property of either the inputs or the outputs of that algorithm. The definition of differential privacy has a universal quantifier over its inputs: for all pairs of inputs that differ in at most one record, the probabilities of any outcome have to be boundedly similar. The probability is taken only over the internal randomness of the algorithm. Since it is a worst-case guarantee with respect to the data, the datasets are not random variables.
