The answer in this question defined how to calculate the probability of rotational cryptanalysis on modulo multiplication $\odot$. This paper defined an algebraic equation of how to calculate the rotational probability of modular addition $\boxplus$ which is
$$ \textbf{P}(\overrightarrow{X\boxplus Y} = \overrightarrow{X}\boxplus\overrightarrow{Y}) = \frac{1}{4}(1+2^{-r} + 2^{r-n}+ 2^{-n}) $$ where $r$ is rotational value and smaller than modular value $n$
and experimental results of 8-bit ($n$) addition shows similar values of
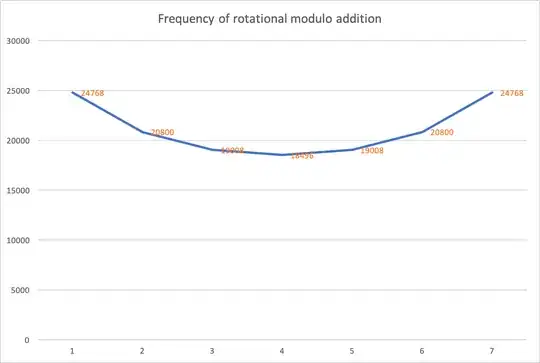
$$ \begin{array}{c|c} r & f \\ \hline 0 & 65536 \\ 1 & 24768 \\ 2 & 20800 \\ 3 & 19008 \\ 4 & 18496 \\ 5 & 19008 \\ 6 & 20800 \\ 7 & 24768 \\ \end{array} $$
where f is the frequency of $ \overrightarrow{X\boxplus Y} = \overrightarrow{X}\boxplus\overrightarrow{Y} $ for each $r$ . the probability of 1 bit rotation is $\frac{24768}{65536}$ is around $.378$ (nearly same as in the table in ). the other thing is you find reflection of frequency values , 1 bit rotation is equal to 7 bit rotation (2 and 6 so on). The following figure shows a flipped bell distribution of rotational modulo addition.
The next step
I conducted the same experiment (8 bit size) but with the following equation (double rotation).
$$ \overrightarrow{X} \odot \overrightarrow{Y} = \overrightarrow{\overrightarrow{(X\odot Y)}} $$ the following table shows the frequency:
$$ \begin{array}{c|c} r & f \\ \hline 0 & 65536 \\ 1 & 4730 \\ 2 & 1082 \\ 3 & 904 \\ 4 & 1664 \\ 5 & 904 \\ 6 & 1082 \\ 7 & 4730 \\ \end{array} $$
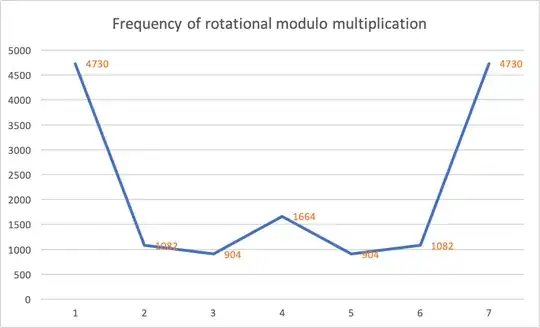from the table and figure, i see there is a reflection of frequency values (suggesting a similar equation of rotational cryptanalysis probability is applied as following:
$$ \textbf{P}(\overrightarrow{X} \odot \overrightarrow{Y} = \overrightarrow{\overrightarrow{(X\odot Y)}}) = \frac{1}{t}(1+2^{-e_0} + 2^{e_0-e_1}+ 2^{-e_1}) $$
Question
if my guess is right , how to calculate the $t , e_0 , e_1$ values?
NOTE Iam happy to share the source code in the question.
