Does the double-hash H(H(x)) have greater collision probability than H(x)?

Question

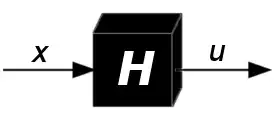
Let $H$ be a collision resistant hash function and $P_c[H](S)$ the collision probability about a sample set $S$ of input elements (eg. random numbers). It increases with double hash? That is,
$P_c[H\circ H](S) \ge P_c[H](S)$ ?

Well... we need a precise $P_c$ definition. Perhaps the problem here is also the choice of a good probability definition (see notes below).

NOTES

Answer's application: the answer is important in the context of checksums used for digital preservation integrity of public files.

Imagine the checksum (the hash digest $H(x)$) of a PDF article of PubMed Central or arxiv.org... And that we need to ensure the integrity, with no "PDF atack" or minimizing it, in nowadays and in a far future, ~20 years.

If the answer is "YES there are a little increase", the recommendation will be "please don't use double-hashing as standard for checksum for PMC or arxivOrg".

General probaility

The general collision probability is defined as

Given $k$ randomly generated $x$ values, where each $x$ is a non-negative integer less than $N$, what is the probability that at least two of them are equal?

and depends only of the $|S|$, so $P_c[H\circ H] = P_c[H]$...
There are a hypothesis of "perfect hash function", but I want to metric the imperfections.

If there are no error on my interpretations, I need other probability definition.

Counting the collisions

Suppose a kind of "collision tax", $\frac{N_c}{|S|}$, based on the number of collisions $N_c$ occured with a specific sample.
So, for many different sample sets $S_i$ with same number of elements, $k=|S_1|=|S_2|=... =|S_i|$. Suppose a set $K$ of all sets $S_i$ and $P_c[H](K)$ as an average of this collision rate.

This kind of probability seems better to express the problem.

... Bloom filter efficiency

Another metric, instead a probability. Perhaps using Bloom filter theory as reference. A kind of efficiency-benchmark of two Bloom filters, one with $H$ other with $H\circ H$.

score 5 · Answer 1 · answered Apr 21 '18 at 12:39

I'm not sure what the question here is, but obviously applying the hash function twice can never decrease the number/probability of collision as all collisions in the first invocation are maintained.

However if H is collision free( a permutation as opposed to a random function) doubling will not cause any more collision it will remain collision free. So we see the number of collision does not strictly increase.

For a PRF, the number of collision does clearly increase, this is one reason why when we iteratively hash passwords in for key derivation we mix in the input again every round and not simply hash calculate $H^n(salt || pass)$

If you look at the structure of a function you will see several cycles and threads(trees) leading into these cycles:

The cycles do not generate more collisions when doubled. Each thread meeting a cycle contributes one collision, If All the threads are of length 1 no more collisions are added when applying twice in any other case the number of collisions increases.

Peter Krauss · Accepted Answer · 2018-05-03T11:39:51.823

Complete answer for dummies

Using the @MeirMaor answer as starting point, there are good clues and illustration.

Using also the concepts of "bad hash function" (instead "good" ones like SHA3) and the "empyrical metric for collision rates" concept of this other question/answer.

Modeling

Suppose $H$ as a black box — and the two connected boxes, $H \circ H$, for our purposes will also be a black box.

So, we need to check it by experiments and some statistical analysis of the experimental results.

Suppose also some "metric" as defined here... There are a sample $S$ where some number of collisions $c>0$ arrives,
$Pr_c[H]=\overline{c}/|S|$
and we do same experiment many times with sample sets with same size $|S|$, so we have an averaged $\overline{c}$.

Let $U=\{u=H(x)|\forall x\}$ and $|S|$ is not so large, that is $|S|<<|U|$.

In that context the main differences between $H$ and $H \circ H$ and valid hypothesis are:

The doubling will not reduce the number of collisions. $Pr_c[H] \le Pr_c[H \circ H]$.
There are no warranty that doubling cause will not cause new collisions, so we can suppose that it will occur.

Representing the first hashing as a set of points (no matter if there was or not a collision, as hypothesis-1), and the second hashing a transition from a point to other point in the same space.

(the illustration is exaggerating, the very most frequent is node-arc-node)

Answering

As showed by the illustration, a good metric is the simple counting of collisions $\overline{r}$ in the second hashing (red dots),
$Pr_r[H]=\overline{r}/|S|$
and ignoring any collision of the first:

if $Pr_c[H]=0$ we can't assert anything, no red dots in the experiment.
"Good hashes" like SHA3 or SHA256 are in this group.
if $Pr_c[H]>0$, a "bad hash", we can assert that $Pr_r[H]>0$
as showed by the illustration, we expect red dots.

We conclude that the answer to the question is afirmative when $|S|<<|U|$ and $H$ is a "bad hash". That is, doubling "bad hashes" will always increase the collision rate probability.

PS: as @SqueamishOssifrage remembered here, to avoid the "nothing to say" we can study simplified versions of hash families,

... we structure the hash family to iterate some internal scrambling function for a variable number of rounds, and study a progression of numbers of rounds...

The reduced-round versions of "good hashes", like BLAKE or SHA3, can be imagined as "bad hash" in the above method.

As reduced-round versions have the same behaviour, accepting the induction, the answer to the question will be afirmative also for "good hashes" (!).

When $|S|$ is bigger, e.g., 1% of $|U|$, even with "good" $H$ we have some non-zero probabiity of collision, so the illustration is self-evident: we can assert that $Pr_r[H]>0$, or directly that $Pr_c[H] < Pr_c[H \circ H]$.

Rigour and other considerations

General considerations, trying to consolidate @SqueamishOssifrage comments:

In the first hashing the domain of $H$ is larger than its codomain.
In the second hashing the domain and codomain have the same size.
(preventing against length extension attacks)
${Pr}_c[H]$ is never zero, not even for SHA-256... But is a so small $\epsilon$.
For "good hashes" the afirmative answer has no practical application: both values, of ${\epsilon}_1=Pr_c[H]$ and ${\epsilon}_2=Pr_c[H \circ H]$, are so minuscule it is silly to worry about ${\epsilon}_2-{\epsilon}_1$.

Semantic: the point about "collision probability" versus "collision resistance" cannot be emphasized enough... See comments (or please edit here, it is a Wiki!).