In RSA $(e,n)$, $(d,p,q)$, why does it work even if plaintext $M$ is not coprime with $n$?

Question

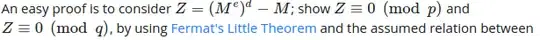
I read this post Does RSA work for any message M?, but I cant prove that $(M^e)^d-M\equiv 0\pmod{p}$ like this:

Answer 1

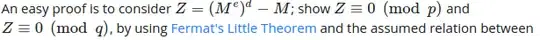
By construction, we have $ed\equiv 1\pmod{\lambda(n)}$, hence $ed\equiv1\pmod{\lambda(n)}$ since $\lambda(p)=p-1$ divides $\lambda(n)=\operatorname{lcm}(p-1,q-1)$. Fermat's little theorem thus implies that $(M^e)^d-M\equiv M^{ed}-M\equiv0\pmod p$ for any $M\in\mathbb Z$.

Answer 2

Let $p$ be a prime. Fermat Little Theorem says that for any integer $a$ co-prime to $p$ (i.e., such that $\gcd(a,p) = 1$), one has $a^{p-1} \equiv 1 \pmod {p}$.

For RSA, we have $ed \equiv 1 \pmod{(p-1)}$ and thus there exists an integer $k$ such that $ed = 1 + k(p-1)$.

There are two cases:

1. if $\gcd(M,p) = 1$ then $M^{ed} \equiv M^{1 + k(p-1)} \equiv M \cdot M^{k(p-1)} \equiv M \cdot (M^{p-1})^k \equiv M \cdot 1^k \equiv M \pmod p$ by Fermat Little Theorem;
2. if $\gcd(M,p) \neq 1$ then $M$ is a multiple $p$ (or equivalently $M \equiv 0 \pmod p$) and thus $M^{ed} \equiv 0^{ed} \equiv 0 \equiv M \pmod p$.

In both cases, we thus have $M^{ed} \equiv M \pmod p$.

For RSA, since we also have $ed \equiv 1 \pmod{(q-1)}$, it can be shown in the same way that $M^{ed} \equiv M \pmod{q}$.

By Chinese remaindering, we thus have $M^{ed} \equiv M \pmod N$ where $N = pq$.