How does Bluetooth pairing (SSP with numeric comparison) work?

Question

I have a question concerning the pairing of two Bluetooth devices using Simple Secure Pairing with numeric comparison. The NIST document I am looking at states on page 14:

Numeric Comparison was designed for the situation where both Bluetooth devices are capable of displaying a six-digit number and allowing a user to enter a “yes” or “no” response. During pairing, a user is shown a six-digit number on each display and provides a “yes” response on each device if the numbers match. Otherwise, the user responds “no” and pairing fails. A key difference between this operation and the use of PINs in legacy pairing is that the displayed number is not used as input for link key generation. Therefore, an eavesdropper who is able to view (or otherwise capture) the displayed value could not use it to determine the resulting link or encryption key.

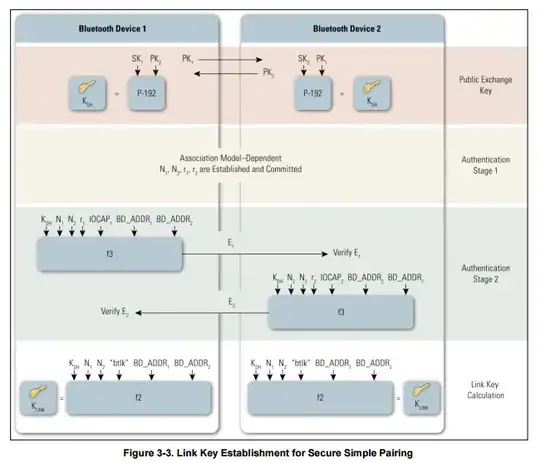
And on page 15, there is a graphic that illustrates the “Link Key Establishment for Simple Secure Pairing”:

Now…

To check on things, I've used a Bluetooth packet capture to sniff the traffic on my phone to see the pairing details. I expected the Bluetooth packet capture to log the details about the $PK$ that was sent and received by the controller. I do see the User Confirmation Request containing the number for the numeric comparison, but I am not able to detect any infos about a $PK$ exchange – as if such an exchange never happened. Therefore, it would be nice to get a confirmation if Simple Secure Pairing indeed uses a $PK$ – and at what point it actually exchanges it.

TL;DR:

I don't understand how the “Link Key Establishment for Simple Secure Pairing” prevents a MITM attack. It seems as if attackers could send a false $PK_2$ nevertheless… or did I miss something?

Answer 1

I think that you miss the point of this method. You can think of this SSP as a key-exchange protocol between two devices which have nothing shared between them a priori and also the entire communication is inspectable and even temperable, that is, the adversary can modify/send messages as it wishes. The big advantage of this SSP method over a usual key-exchange protocols (i.e. between computers over the Internet) is that the devices have a human linking between them, or abstractly, authenticated communication channel that cannot be tampered with by the adversary and can be used to send a short message.

Regarding the MITM attack, I'm not very familiar with the spec but looking at this makes it more clear: Assume that as an attacker you execute this key-exchange protocol with both devices A and B. Let $pk_A, pk_B$ be the public keys of A and B resp. and let $pk_A',pk_B'$ be the keys that you (the adversary) choose in the execution between you and A and between you and B resp. Now the number that appears on the screen is a function $H$ (truncated as needed) applied to the keys of the parties (and some more random strings but let's skip it for simplicity), that is, the number on A's device would be $c_A=H(pk_A,pk_A')$ (where the adversary behaves as device B) and the number on B's device would be $c_B=H(pk_B',pk_B)$ (where the adversary behaves as device A). The goal of the adversary is to make $c_A=c_B$ in order for the device to be "paired". The randomness of $pk_A$ dictates that $c_A$ is random as well, which means that in order to make $c_B=c_A$ the adversary has to find a $pk_B'$ such that $c_A=H(pk_B',pk_B)$. This is a hard problem (as finding a preimage for a hash function) and thus the MITM attack could not be held successfully.