reducing false positives in searchable encryption

Question

Practical techniques for searchable encryption proposed by Song et al. [1] have a false positive rate of $l/2^m$ where $l$ is left half of encrypted bits and $m$ is right half and $l+m=n$ where $n$ is number of bits of the word being encrypted. For getting clarity on these bits please refer the figure 3 in page 6. (paper). 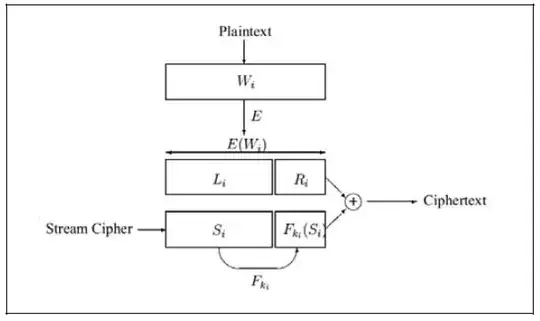Especially when the input domain of words being encrypted is not so random say serial numbers, sequence ids etc. the false positives are simply high.

Is there any subsequent work done or techniques available for reducing the false positive rate ?

---

_{[1] – Song, Dawn Xiaoding, David Wagner, and Adrian Perrig. "Practical techniques for searches on encrypted data." Security and Privacy, 2000. S&P 2000. Proceedings. 2000 IEEE Symposium on. IEEE, 2000.}

Answer 1

Additional Storage approach

A trivial way is with additional storage. by making the $l$ to be complete string instead of few $left$ bits shown in the figure above. so technically $|l|=|n|$ and $|m| = 0$.

This way the entire string is covered for search. Now rest of the scheme is same except that the stream cipher bits $S_i$ in the figure above are $\oplus$'ed with entire $l_i$ and store the encryption of $F_{ki}(S_i)$ separately for matching. Now there is an additional over head of storing $F_{ki}(S_i)$ bits. In reality, if we use AES for $F_{ki}(S_i)$ operation would result in 128 bits additionally which might be an over kill. If we use some length preserving encryption like FNR we could reduce the size of additional storage needed to size of word itself. Even in this case, we need double the storage of input text as premium for reducing false positives.

Not sure of any other approaches so far. I have made a quick proof-of-concept which could be found here. The test cases written for both that has false positives and also that will not have any but needs additional storage