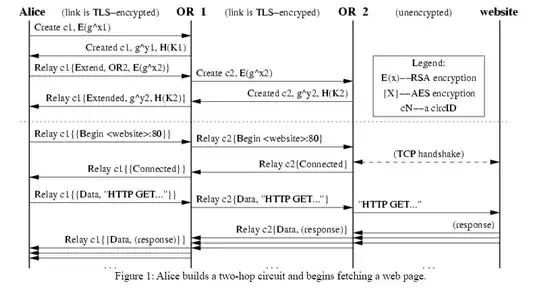
I am currently exploring the workings of the Tor network, specifically how the Diffie-Hellman (DH) key exchange protocol is employed to establish shared secret keys between the client and each relay in the circuit.
In this lesson from Nick Mathewson (https://youtu.be/OgGTJIgNewE?si=ft3a0Y0Brgtuj5eF&t=2035) it is explained, what I do not understand is how the key is generated from client and node 2 without letting entry node to know what client and node 2 are sharing.
From the paper "Tor: The Second-Generation Onion Router" https://svn-archive.torproject.org/svn/projects/design-paper/tor-design.html , in section 4 "The Tor Design" is explained too
It says: To extend the circuit further, Alice sends a relay extend cell to Bob, specifying the address of the next OR (call her Carol), and an encrypted g^x2 for her. Bob copies the half-handshake into a create cell, and passes it to Carol to extend the circuit. (Bob chooses a new circID CBC not currently used on the connection between him and Carol. Alice never needs to know this circID; only Bob associates CAB on his connection with Alice to CBC on his connection with Carol.) When Carol responds with a created cell, Bob wraps the payload into a relay extended cell and passes it back to Alice. Now the circuit is extended to Carol, and Alice and Carol share a common key K2 = g^x2 y2.
I am seeking clarity on how the client securely shares the encryption key with the middle node and exit node when passing through the previous nodes. How does the client establish a unique shared secret key for communication with each relay in the circuit?
Thank you